PUBLICIDADE
Volume de um cilindro é o que determina a capacidade volumétrica desse sólido, sendo possível determinar o espaço que ele ocupa ou qual a sua capacidade máxima de armazenamento, como é o caso de embalagens e seus conteúdos.
O volume resulta do produto da área da base do cilindro pela sua altura e para ser calculado necessita das medidas do raio da base do cilindro e da altura desse sólido.
Leia também: Como calcular o volume da esfera?
Tópicos deste artigo
- 1 - Resumo sobre o volume do cilindro
- 2 - Videoaula sobre o volume do cilindro
- 3 - O que é cilindro?
- 4 - Qual a fórmula do volume do cilindro?
- 5 - Como calcular o volume do cilindro?
- 6 - Exercícios resolvidos sobre o volume do cilindro
Resumo sobre o volume do cilindro
-
O cilindro é um corpo redondo constituído de duas bases paralelas em formato circular e segmentos de reta com extremidades nesses círculos.
-
Sabendo o raio da base do cilindro e a altura dele, é possível calcular seu volume.
-
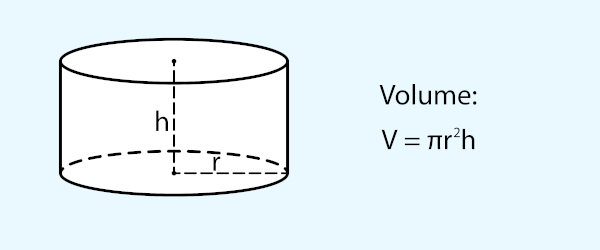
O volume do cilindro de altura h e raio da base r é dado por: \(V=π⋅r^2⋅h\).
Videoaula sobre o volume do cilindro
O que é cilindro?
O cilindro é um sólido geométrico classificado como um corpo redondo. É formado por duas bases circulares congruentes (com mesma medida do raio) contidas em dois planos paralelos distintos e pela reunião de todos os segmentos de reta cujas extremidades pertencem aos círculos e são paralelos ao segmento que une os centros desses círculos.
Qual a fórmula do volume do cilindro?
A medida do volume do cilindro corresponde à capacidade máxima que esse sólido geométrico consegue comportar.
Para calcular o volume do cilindro é necessário conhecer ou possuir meios de determinar duas de suas medidas: o raio r do círculo de sua base e a altura h do cilindro, que representa a distância dos planos paralelos que contém cada uma das bases.
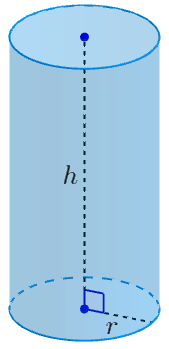
O volume do cilindro é o produto da área de sua base pela altura desse sólido. Sabendo que a base de um cilindro é um círculo, a fórmula para determinar seu volume pode ser escrita da seguinte forma:
Volume do cilindro = Área da base ⋅ Altura
V = Área do círculo ⋅ Altura
\(V = π⋅r^2⋅h\)
Como calcular o volume do cilindro?
Sabendo as medidas da altura do cilindro e do raio de sua base, é possível utilizar a fórmula do volume vista anteriormente para encontrar a capacidade desse cilindro.
Veja agora alguns exemplos de como utilizá-la.
-
Exemplo: Calcule o volume de um cilindro cuja altura mede 10 cm e o diâmetro da base mede 4 cm. (Utilize π ≈ 3,14)
Neste caso, o problema fornece a altura e diâmetro da base do cilindro. Lembrando que o raio de uma circunferência equivale à metade do diâmetro, conclui-se que o raio da base do cilindro mede 2 cm.
Por fim, com os dados encontrados, basta substituí-los na fórmula:
\(V = π⋅r^2⋅h\)
\( V = π⋅(2)^2⋅10\)
\( V ≈ 3,14⋅4⋅10\)
\(V ≈ 125,6\ cm^3\)
Leia também: Como calcular o volume do cubo?
Exercícios resolvidos sobre o volume do cilindro
Questão 1
(Enem 2020) Uma loja de materiais de construção vende dois tipos de caixas-d’água: tipo A e tipo B. Ambas têm formato cilíndrico e possuem o mesmo volume, e a altura da caixa-d’água do tipo B é igual a 25% da altura da caixa-d’água do tipo A.
Se R denota o raio da caixa-d’água do tipo A, então o raio da caixa-d’água do tipo B é
a) \(\frac{R}2\)
b) 2R
c) 4R
d) 5R
e) 16R
Resolução
Para calcular o volume de um cilindro, precisamos saber sua altura e o raio de sua base. Neste caso, a caixa-d’água A possui raio de medida R, e vamos denotar sua altura por hA. Já a caixa-d’água B possui raio que vamos denotar por r e altura igual a 25% da altura da caixa A, ou seja,
Altura da caixa-d’água \(B = h_B=\frac{25}{100}⋅h_A=\frac{1}4 h_A\)
Além disso, o volume das caixas é o mesmo, ou seja, VA = VB.
Com esses dados, podemos utilizar a fórmula de volume do cilindro e igualar esses dois volumes:
\(V_A=V_B\)
\(π⋅R^2⋅h_A=π⋅r^2⋅h_B\)
\(R^2⋅h_A=r^2⋅\frac{1}4 h_A\)
\(R^2=r^2⋅\frac{1}4\)
\(r^2=4⋅R^2\)
\(r=2⋅R\)
A alternativa correta é a alternativa b.
Questão 2
(Enem 2015) Para resolver o problema de abastecimento de água foi decidida, em uma reunião do condomínio, a construção de uma nova cisterna. A cisterna atual tem formato cilíndrico, com 3 m de altura e 2 m de diâmetro, e estimou-se que a nova cisterna deverá comportar 81 m3 de água, mantendo o formato cilíndrico e a altura da atual. Após a inauguração da nova cisterna, a antiga será desativada. Utilize 3,0 como aproximação para π.
Qual deve ser o aumento, em metros, no raio da cisterna para atingir o volume desejado?
a) 0,5
b) 1,0
c) 2,0
d) 3,5
e) 8,0
Resolução
Para resolver essa questão, é necessário saber a medida do raio da antiga cisterna e da nova. Como o diâmetro da antiga cisterna é de 2 m, então o raio dela é metade disso, ou seja, a antiga cisterna possui 1 m de raio.
Sobre a nova cisterna, o problema indica o valor de sua altura (que é o mesmo da antiga, ou seja, 3 m) e fornece o seu volume, de 81 m3.
Assim, pela fórmula do volume, isolando a medida do raio r :
\(V = π⋅r^2⋅h\)
\(81 = 3,0⋅r^2⋅3\)
\(\frac{81}9 = r^2\)
\(r^2=9\)
\(r=3\ m\)
Fazendo a diferença entre o raio da nova cisterna e da antiga, chega-se em \(3-1=2\) metros.
A alternativa correta é a alternativa c.
Fontes
ALMEIDA, Célio Pinto de. Geometria espacial. 1. ed. Rio de Janeiro: G. Ermakoff, 2018.
DOLCE, Osvaldo; NICOLAU, José. Fundamentos de matemática elementar 10 – Geometria espacial. 5. ed. Santos: Atual, 1993.
Por Lenon Ávila
Professor de Matemática