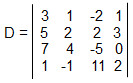PUBLICIDADE
Para o cálculo de determinantes de matrizes quadradas de ordem menor ou igual a 3 (n≤3), temos algumas regras práticas para realizar estes cálculos. Entretanto, quando a ordem é superior a 3 (n>3), muitas destas regras não são aplicáveis.
Por isso veremos o teorema de Laplace, que, utilizando o conceito do cofator, conduz o cálculo dos determinantes para regras que se aplicam a quaisquer matrizes quadradas.
O teorema de Laplace consiste em escolher uma das filas (linha ou coluna) da matriz e somar os produtos dos elementos dessa fila pelos seus respectivos cofatores.
Ilustração algébrica:
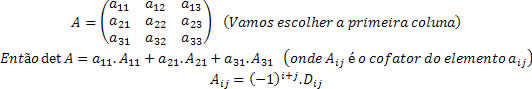
Vejamos um exemplo:
Calcule o determinante da matriz C, utilizando o teorema de Laplace:
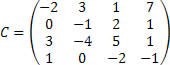
De acordo com o teorema de Laplace, devemos escolher uma fila (linha ou coluna) para calcular o determinante. Vamos utilizar a primeira coluna:
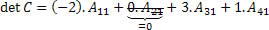
Precisamos encontrar os valores dos cofatores:
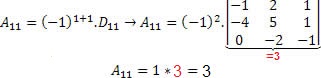
.jpg)
.jpg)
Sendo assim, pelo teorema de Laplace, o determinante da matriz C é dado pela seguinte expressão:
.jpg)
Note que não foi preciso calcular o cofator do elemento da matriz que era igual a zero, afinal, ao multiplicarmos o cofator, o resultado seria zero de qualquer forma. Diante disso, quando nos depararmos com matrizes que possuem muitos zeros em alguma de suas filas, a utilização do teorema de Laplace se torna interessante, pois não será necessário calcular diversos cofatores.
Vejamos um exemplo deste fato:
Calcule o determinante da matriz B, utilizando o teorema de Laplace:
.jpg)
Veja que a segunda coluna é a fila que possui maior quantidade de zeros, portanto utilizaremos esta fila para calcular o determinante da matriz através do teorema de Laplace.
.jpg)
Portanto, para determinar o determinante da matriz B, basta encontrar o cofator A22.
.jpg)
Sendo assim, podemos finalizar os cálculos do determinante:
det B = (- 1) . (- 65) = 65
Por Gabriel Alessandro de Oliveira
Graduado em Matemática
Equipe Brasil Escola