PUBLICIDADE
Para iniciar o estudo de números binomiais é necessário relembrar situações que envolvem produtos notáveis. Com base na expressão (x + y)n iremos calcular as expressões seguintes considerando n ≤ 3.
(x + y)0 = 1
(x + y)1 = x + y
(x + y)2 = x2 + 2xy + y2
(x + y)3 = x3 +3x2y + 3xy2 + y3
Com base no desenvolvimento das expressões onde n ≤ 3, podemos estabelecer uma relação para cálculos quando n > 3. Observe:
(x + y)4 = (x + y)(x + y)3 = (x + y)*( x3 +3x2y + 3xy2 + y3)
x4 + 3x3y + 3x2y2 + xy3 + x3y + 3x2y2 + 3xy3 + y4
x4 + 4x3y + 6x2y2 + 4xy3 + y4
De acordo com que n > 3, os cálculos começam a ficar mais complexos e trabalhosos. Para cálculos em que n assume valores elevados, usamos a definição do binômio de Newton, mas antes precisamos conhecer algumas técnicas para adentrarmos em tal conteúdo.
Podemos definir os coeficientes binomiais através da seguinte generalização:
![]()
com n Є N, m Є n e m ≤ n.
Situações particulares
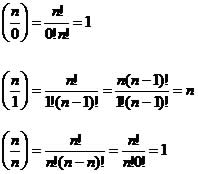
Destacamos que os coeficientes binomiais serão de grande importância na utilização da seguinte expressão
(x + y)n
Triângulo de Pascal
Os coeficientes binomiais podem ser organizados num triângulo denominado triângulo de Pascal ou de Tartaglia.

Note na organização do triângulo, pois os numeradores iguais se encontram numa mesma linha e os denominadores iguais se encontram numa mesma coluna.
Substituindo os binomiais pelos seus respectivos valores:

Soma dos elementos por linha no triângulo de Pascal:
Linha 1 = 1 = 20
Linha 2 = 1 + 1 = 2¹
Linha 3 = 1 + 2 + 1 = 4 = 2²
Linha 4 = 1 + 3 + 3 + 1 = 8 = 2³
Linha 5 = 1 + 4 + 6 + 4 + 1 = 16 = 24
Linha 6 = 1 + 5 + 10 + 10 + 5 + 1 = 32 = 25
e assim sucessivamente.
Binômio de Newton
Vamos substituir os termos x por a e y por b na expressão (x + y)n no intuito de diferenciar os elementos da expressão da parte literal dos polinômios que serão apresentados e trabalhados, passando a ter a expressão
(a + b)n .
De acordo com o binômio de Newton, temos a seguinte forma geral para o desenvolvimento das expressões na forma (a + b)n, com n > 3:
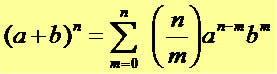
Desenvolva (4x + 2)5 utilizando o binômio de Newton.
.jpg)
1*1024x5 * 1 + 5*256x4 * 2 + 10*64x3 * 4 + 10*16x2 * 8 + 5*4x * 16 + 1*1 * 32
1024x5 + 2560x4 + 2560x3 + 1280x2 + 320x + 32
(4x + 2)5 = 1024x5 + 2560x4 + 2560x3 + 1280x2 + 320x + 32
Por Marcos Noé
Graduado em Matemática






