A hipérbole é uma cônica, ou seja, é uma das figuras obtidas pela secção de um cone duplo de revolução. A parábola, a circunferência e a elipse são outros tipos de cônicas.
Considere dois pontos fixos, F1 e F2, e um número real positivo a. Todos os pontos P que satisfazem a relação abaixo compõem a hipérbole de focos F1 e F2:
|d(P,F1)−d(P,F2)|=2a
Leia também: Geometria analítica — área que estuda as formas geométricas com o auxílio da álgebra
Tópicos deste artigo
- 1 - Resumo sobre hipérbole
- 2 - O que é hipérbole?
- 3 - Elementos da hipérbole
- 4 - Qual a fórmula da hipérbole?
- 5 - Como fazer uma hipérbole?
- 6 - Para que serve a hipérbole na Matemática?
- 7 - Exercícios resolvidos sobre hipérbole
Resumo sobre hipérbole
- A hipérbole é uma cônica, assim como a circunferência, a parábola e a elipse.
- Dados dois pontos, F1 e F2, com distância 2c e um número real positivo a, com a < c , chamamos de hipérbole o conjunto de pontos P tais que
|d(P,F1)−d(P,F2)|=2a
- O ponto médio entre os focos F1 e F2 é chamado de centro da hipérbole.
- Se os focos F1 e F2 estão sobre o eixo horizontal, então a equação da hipérbole é
x2a2−y2b2=1
- Se os focos F1 e F2 estão sobre o eixo vertical, então a equação da hipérbole é
− x2a2+y2b2=1
O que é hipérbole?
Considere F1 e F2 pontos fixos de distância 2c e a um número real positivo tal que a < c . A hipérbole é o conjunto de pontos P tais que a diferença em módulo das distâncias até F1 e F2 seja igual a 2a. Em notação matemática, escrevemos que os pontos P da hipérbole são tais que
|d(P,F1)−d(P,F2)|=2a
em que d(P,F1) é a distância entre P e F1 e =d(P,F2) é a distância entre P e F2.
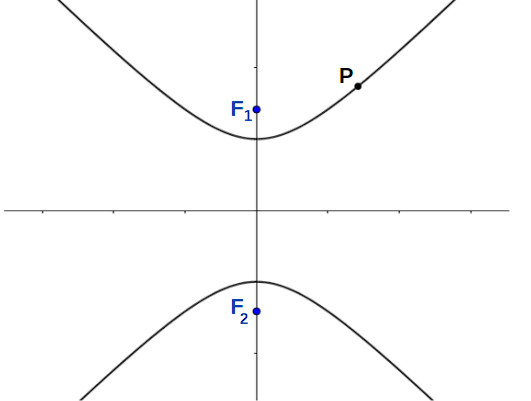
Perceba que a hipérbole é formada por dois “pedaços”, chamados de ramos. Um dos ramos contém os pontos P cuja distância aos focos é positiva, ou seja, d(P,F1)−d(P,F2)=2a. O outro ramo possui os pontos P cuja distância aos focos é negativa, ou seja, d(P,F1)−d(P,F2)=− 2a.
Elementos da hipérbole
Para compreender a hipérbole, é fundamental conhecer os elementos que a compõem.
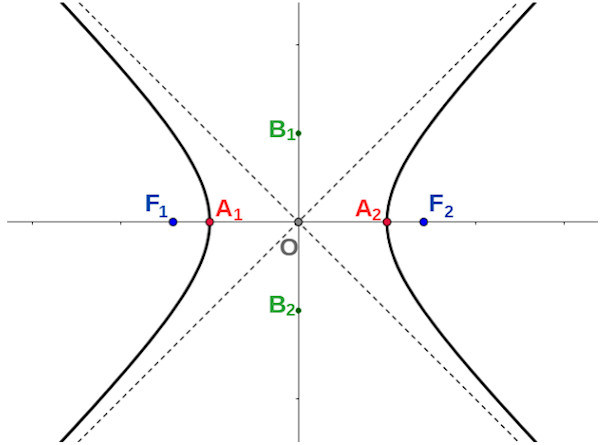
- F1 e F2 são os focos da hipérbole.
- A1 e A2 são os vértices da hipérbole.
- O é o centro da hipérbole e é ponto médio do segmento F1F2.
- O segmento F1F2 é o segmento focal, e seu tamanho, de medida 2c, é chamado de distância focal. Assim, OF1=OF2=c .
- O segmento A1A2 é o eixo real e possui tamanho de medida 2a. Assim, OA1=OA2=a.
- Os pontos B1 e B2 são tais que B1A1=B1A2=B2A1=B2A2=c.
- O segmento B1B2 é o eixo imaginário (ou conjugado) e possui tamanho de medida 2b. Assim, OB1=OB2=b.
- As retas pontilhadas são assíntotas à hipérbole.
Observação 1: Os segmentos com medida a, b e c podem ser relacionados pelo teorema de Pitágoras. Perceba que o triângulo B1OA2 é retângulo em O com OB1=b, OA2=a e B1A2=c . Assim, c2=a2+b2.
Observação 2: Note que na imagem trabalhada nesse tópico, os focos estão sobre o eixo horizontal e na imagem do tópico anterior os focos estão sobre o eixo vertical. Estes são alguns exemplos do formato de uma hipérbole, mas os focos podem ser pontos do plano cartesiano que não pertencem aos eixos x e y.
Leia também: Parábola — tipo de cônica que representa uma função do 2º grau
Qual a fórmula da hipérbole?
A fórmula da hipérbole é uma expressão que descreve os pontos P=(x,y) da hipérbole. Essa expressão é chamada de equação da hipérbole e depende da localização dos focos.
Por uma questão de simplicidade, vamos conhecer as equações (reduzidas) da hipérbole para focos sobre o eixo vertical e horizontal.
-
Caso 1: focos F1 e F2 sobre o eixo horizontal (eixo do x)
Nessas condições, a equação reduzida da hipérbole é
x2a2−y2b2=1
-
Caso 2: focos F1 e F2 sobre o eixo vertical (eixo do y)
Nessas condições, a equação reduzida da hipérbole é
− x2a2+y2b2=1
Como fazer uma hipérbole?
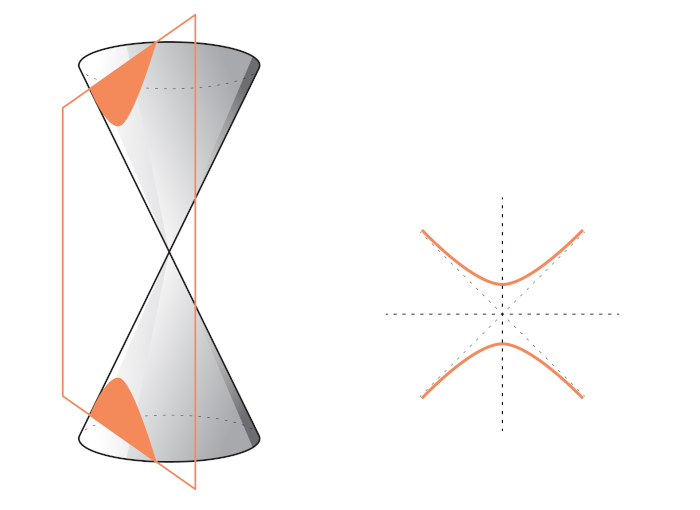
Geometricamente, a hipérbole é obtida pela secção de um cone duplo de revolução de forma paralela ao eixo.
Para que serve a hipérbole na Matemática?
Uma das aplicações da hipérbole é o uso de sua propriedade refletora em espelhos hiperbólicos de telescópios ópticos e radiotelescópios.
Outras aplicações se relacionam com o hiperboloide. O hiperboloide é uma superfície gerada pela revolução de uma hipérbole. O hiperboloide é utilizado na construção de pequenos objetos, monumentos e instalações industriais.

Exercícios resolvidos sobre hipérbole
Questão 1
Considere F1=(−2,0) e F2=(2,0) os focos de uma hipérbole com eixo real de medida 2. A equação reduzida dessa hipérbole é
a) x22−y2=1
b) x23−y2=1
c) x2−y23=1
d) x2−y22=1
e) x2−2y2=1
Resolução
Note que 2c = 4 e 2a = 2 . Assim, c = 2 e a = 1 . Como c2=a2+b2 , temos que b=3 . Logo, considerando que os focos estão sobre o eixo horizontal, temos que a equação reduzida dessa hipérbole é
x2−y23=1
Alternativa C.
Questão 2
Classifique as informações abaixo em V (verdadeira) ou F (falsa).
I. A hipérbole é uma cônica, assim como a elipse, a circunferência e a parábola.
II. Os focos da hipérbole são pontos que pertencem aos ramos da hipérbole.
III. Considere 2c a distância entre F1 e F2 e a um número positivo menor que c. O conjunto de pontos P tais que |d(P,F1)−d(P,F2)|=2a formam a hipérbole de focos F1 e F2.
A ordem correta, de cima para baixo, é
a) F-F-F
b) F-V-F
c) F-V-V
d) V-F-V
e) V-V-V
Resolução
A única afirmação falsa é a II, pois os focos da hipérbole (pontos F1 e F2) não pertencem aos ramos da hipérbole.
Alternativa D.
Por Maria Luiza Alves Rizzo
Professora de Matemática