A função do 1º grau é uma relação matemática expressa pela fórmula f(x) = ax + b, em que a e b são números reais, e x representa qualquer valor real. O coeficiente a é chamado de coeficiente angular e indica a inclinação da reta que representa o gráfico da função no plano cartesiano, enquanto b é o coeficiente linear e representa o ponto em que essa reta cruza o eixo y.
Para calcular o valor da função, basta substituir o valor de x na expressão e resolver a operação. O gráfico da função do 1º grau é sempre uma reta, que pode ser crescente, quando a é maior que zero, ou decrescente, quando a é menor que zero. O coeficiente linear b mostra o valor de f(x) quando x é igual a zero, sendo o ponto de interseção com o eixo y.
Leia também: Afinal, o que é função?
Tópicos deste artigo
- 1 - Resumo sobre função do 1º grau
- 2 - Videoaula sobre função do 1º grau
- 3 - O que é função do 1º grau?
- 4 - Como calcular função do 1º grau?
- 5 - Gráfico de uma função do 1º grau
- 6 - Mapa mental: gráfico de função do 1º grau
- 7 - Coeficiente linear e angular da função do 1º grau
- 8 - Função crescente e decrescente
- 9 - Exercícios resolvidos sobre função do 1º grau
Resumo sobre função do 1º grau
- A função do 1º grau é a função com lei de formação f(x) = ax + b.
- Na lei de formação, a é o coeficiente angular.
- Na lei de formação, b é o coeficiente linear.
- A função do 1º grau é conhecida também como função afim.
- O gráfico da função de 1º grau é uma reta.
- A reta pode ser crescente ou decrescente.
- Se o coeficiente a for positivo, o gráfico da função é crescente.
- Se o coeficiente a for negativo, o gráfico da função é decrescente.
Videoaula sobre função do 1º grau
O que é função do 1º grau?
Uma função do 1º grau, conhecida também como função afim ou função polinomial do 1º grau, é uma relação matemática que associa, para cada valor de x, um valor f(x) pela lei de formação f(x) = ax + b, em que a e b são números reais, sendo que a é diferente de zero. Na lei de formação da função, temos que:
f(x) = ax + b
a → coeficiente angular
b → coeficiente linear
x → variável independente
f(x) → variável dependente
Como calcular função do 1º grau?
Sabendo a lei de formação da função, é possível determinar o seu valor numérico. Para isso, basta substituir o valor de x na expressão da função e, assim, encontrar a imagem correspondente àquele número.
Exemplo:
Dada a lei de formação:
f(x) = 3x - 5
Calcularemos o valor numérico da função para alguns valores de x:
x = 1
f(1) = 3 · 1 - 5
f(1) = 3 - 5
f(1) = -2
x = 2
f(2) = 3 · 2 - 5
f(2) = 6 - 5
f(2) = 1
x = 3
f(3) = 3 · 3 - 5
f(3) = 9 - 5
f(3) = 4
Veja também: Qual a diferença entre função e equação?
Gráfico de uma função do 1º grau
O gráfico de uma função do 1º grau é uma reta. Como vimos essa reta pode ser crescente ou decrescente. Para a função de 1º grau no gráfico, encontramos pares ordenados (x, y) que satisfazem a lei de formação da função.
Exemplo:
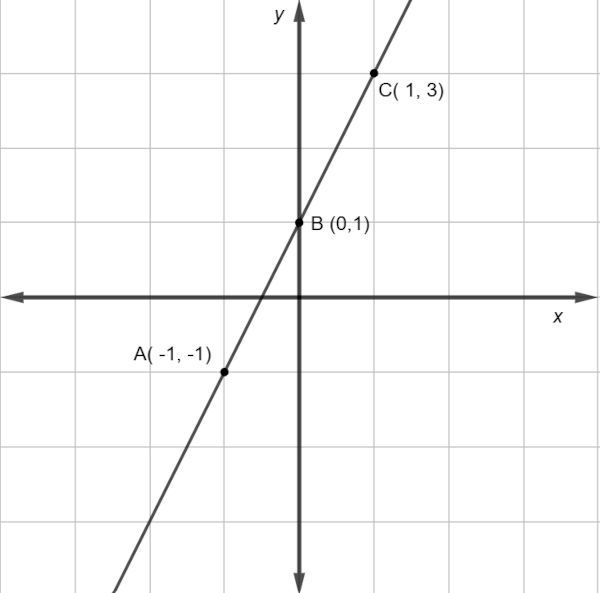
Construa o gráfico da função f(x) = 2x + 1.
Para construir o gráfico, calcularemos alguns valores numéricos da função:
f(−1)=2⋅(−1)+1=−2+1=−1f(0)=2⋅0+1=0+1=+1f(1)=2⋅1+1=2+1=3
Então sabemos que a reta que representa o gráfico dessa função passa pelos pontos A (-1,-1), B (0,1) e C (1,3). No plano cartesiano, traçaremos a reta que passa por esses três pontos.
Mapa mental: gráfico de função do 1º grau
.jpeg)
Baixe o Mapa mental do gráfico de função do 1º grau.
Coeficiente linear e angular da função do 1º grau
O coeficiente angular é o número que acompanha a variável x na função do 1º grau. O coeficiente linear é o termo independente. Representado geralmente por b, ele indica o ponto onde a reta corta o eixo y.
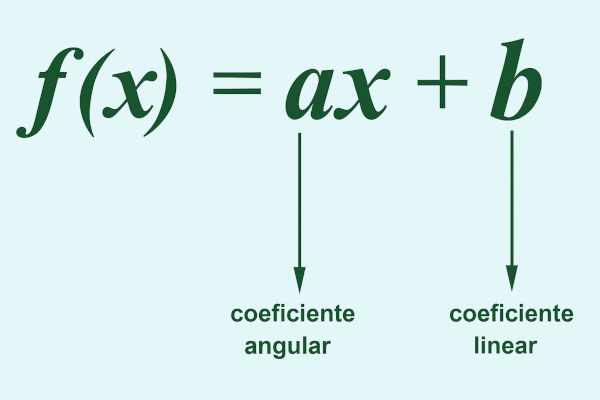
Exemplos:
Dadas as funções a seguir, encontre o valor do coeficiente angular a e do coeficiente linear b.
a) f(x) = 3x - 5
a = 3eb = -5
b) y = -x + 1
a = -1eb = 1
c) f(x) = 2 - 5x
a = -5eb = 2
d) y = x
a = 1eb = 0
O coeficiente angular determina se a função é crescente, decrescente ou constante:
Se a > 0, a função é crescente.
Então se a for positivo, a função é crescente.
Se a = 0, a função é constante.
Então se a for 0, ou seja, a função for f(x) = b, então a função é constante.
Se a < 0, a função é decrescente.
Então se a for negativo, a função é decrescente.
O coeficiente linear é o ponto em que a reta corta o eixo y, é a imagem da função quando x vale zero.
Saiba mais: O que é uma função linear?
Função crescente e decrescente
Existem três comportamentos possíveis para a função afim, que pode ser constante, decrescente ou crescente.
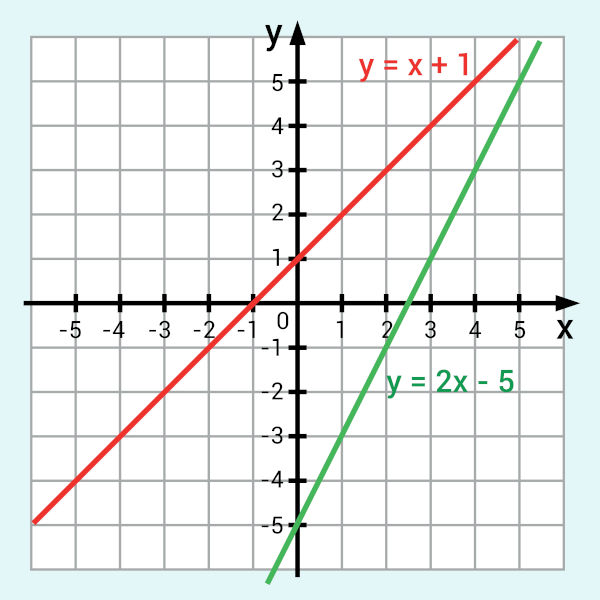
- Função crescente: quando a > 0. Veja, a seguir, o gráfico das funções y = x + 1 e y = 2x – 5, e note que ambas são crescentes.
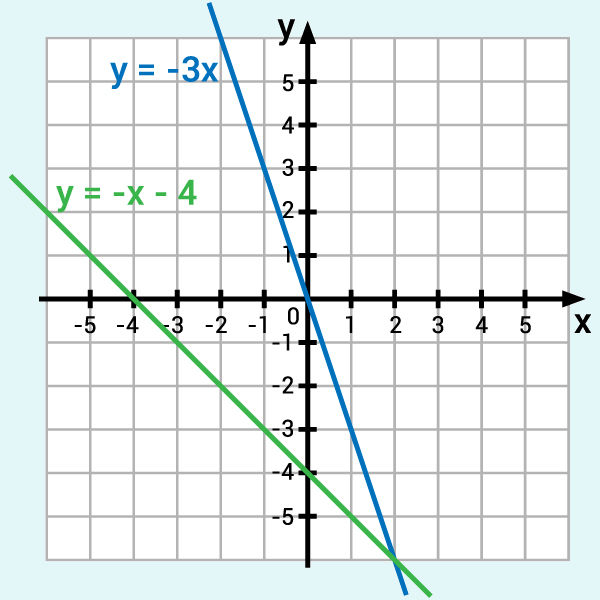
- Função decrescente: quando a < 0. Veja, a seguir, os gráficos das funções decrescentes y = -3x e y = -x – 4.
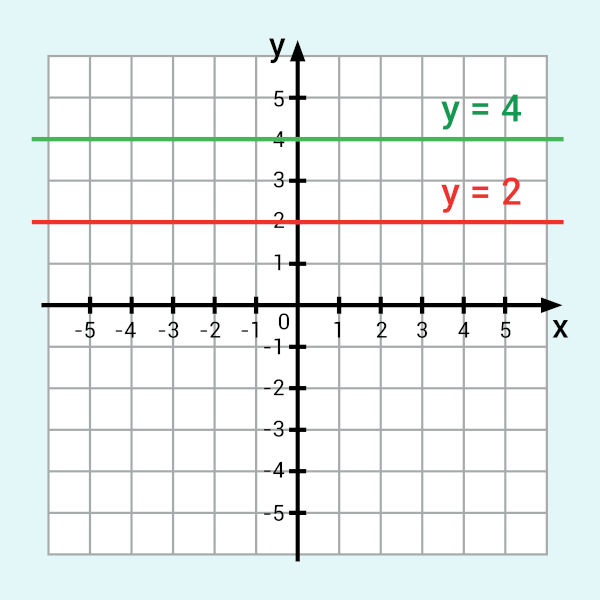
- Função constante: quando a = 0, ou seja, quando a função for y = b. Veja, a seguir, o gráfico das funções y = 4 e y = 2.
Exercícios resolvidos sobre função do 1º grau
Questão 1
Dada a função com lei de formação f(x) = 2x - 5, o valor da imagem da função quando x = 5 é:
- 2
- 3
- 4
- 5
- 6
Resolução:
Alternativa D
Calculando f(5), temos que:
f(5) = 2 · 5 - 5
f(5) = 10 - 5
f(5) = 5
Questão 2
Heitor quer contratar um serviço de TV por assinatura. Ele sabe que o plano básico cobra uma taxa fixa de R$ 50 por mês, além de R$ 5 por cada canal extra que ele contratar.
Represente essa situação por uma função do 1º grau que relacione o valor a ser pago (y) em função do número de canais extras (x).
Depois, calcule o valor que Heitor pagará se contratar 4 canais extras.
A) y = 5x + 50, e ele pagará R$ 70.
B) y = 5x + 50, e ele pagará R$ 80.
C) y = 50x + 5, e ele pagará R$ 30.
D) y = 5x – 50, e ele pagará R$ 20.
E) y = 50x − 5, e ele pagará R$ 40.
Resolução:
Alternativa A
A função do 1º grau que relaciona o valor a ser pago (y) em função do número de canais extras (x) é:
y = 5x + 50
Pois R$ 50 é a taxa fixa e R$ 5 são cobrados a cada canal x.
O valor de 4 canais será:
y = 5 ⋅ 4 + 50
y = 20 + 50
y = 70
Então a lei de formação é y = 5x + 50, e ele pagará R$ 70.
Fontes
BIANCHINI, Edwaldo. Matemática. 7. ed. São Paulo: Moderna, 2011. (9º ano)
IEZZI, Gelson; MURAKAMI, Carlos. Fundamentos de Matemática Elementar – Vol. 1: Conjuntos e funções. 9. ed. São Paulo: Atual Didáticos, 2013.