PUBLICIDADE
A equação reduzida da reta facilita a representação de uma reta no plano cartesiano. Na geometria analítica, é possível realizar essa representação e descrever a reta a partir da equação y = mx + n, em que m é o coeficiente angular e n é o coeficiente linear. Para encontrar essa equação, é necessário conhecer dois pontos da reta, ou um ponto e o ângulo formado entre a reta e o eixo x no sentido anti-horário.
Leia também: O que é reta?
Tópicos deste artigo
- 1 - Qual é a equação reduzida da reta?
- 2 - Coeficiente angular
- 3 - Coeficiente linear
- 4 - Como calcular a equação reduzida da reta
- 5 - Exercícios resolvidos
Qual é a equação reduzida da reta?
Na geometria analítica, buscamos uma lei de formação para descrever figuras planas, como a circunferência, uma parábola, a própria reta, entre outras. A reta possui duas possibilidades de equação, a equação geral da reta e a equação reduzida da reta.
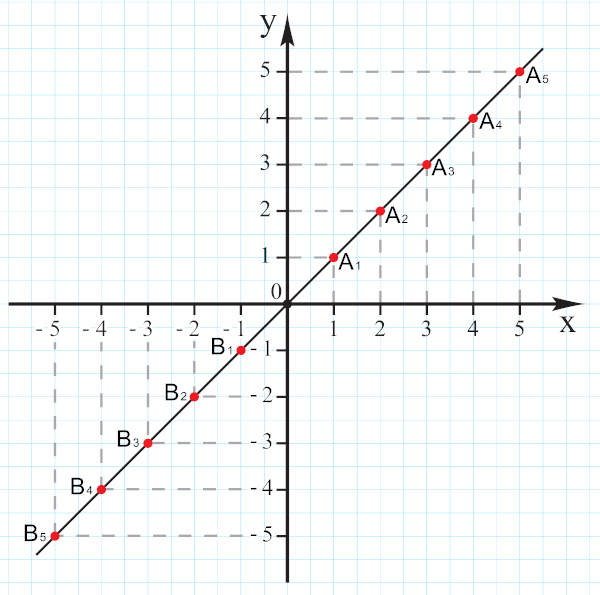
A equação reduzida da reta é y = mx + n, em que x e y são, respectivamente, a variável independente e a variável dependente; m é o coeficiente angular, e n é o coeficiente linear. Além disso, m e n são números reais. Com a equação reduzida da reta, é possível calcular quais são os pontos que pertencem a essa reta e quais não pertencem.
Coeficiente angular
O coeficiente angular nos diz muito sobre o comportamento da reta, pois, a partir dele, é possível analisar a inclinação da reta e identificar se ela é crescente, decrescente ou constante. Além disso, quanto maior o valor do coeficiente angular, maior será o ângulo entre a reta e o eixo x, no sentido anti-horário.
Para calcular o coeficiente angular da reta, existem duas possibilidades. A primeira é saber que ele é igual à tangente do ângulo α:
|
m = tgα |
Sendo α o ângulo entre a reta e o eixo x, conforme a imagem.
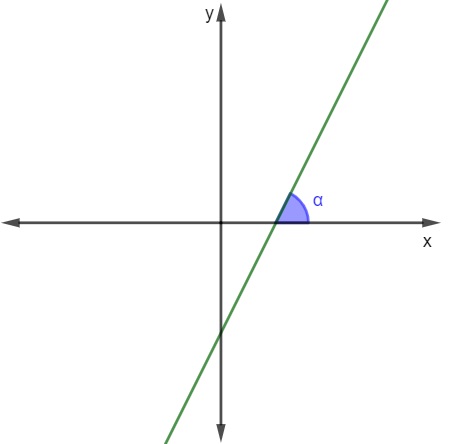
Nesse caso, basta conhecermos o valor do ângulo e calcular a tangente dele para encontrar o coeficiente angular.
Exemplo:
Qual é o valor do coeficiente angular da reta a seguir?
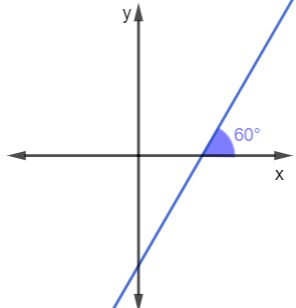
Resolução:
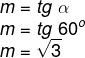
O segundo método para calcular o coeficiente angular é conhecendo dois pontos pertencentes à reta. Seja A(x1,y1) e B (x2,y2), então o coeficiente angular pode ser calculado por:
![]()
Exemplo:
Encontre o valor do coeficiente angular da reta representada no plano cartesiano a seguir. Considere A(-1, 2) e B (2,3).
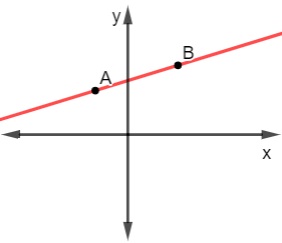
Resolução:
Como conhecemos dois pontos, temos que:
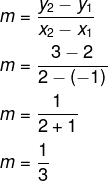
Para tomar a decisão sobre qual método utilizar para calcular o coeficiente angular da reta, primeiro é necessário analisar quais são as informações que temos. Se o valor do ângulo α for conhecido, basta calcular a tangente desse ângulo; agora, se conhecemos somente o valor de dois pontos, nesse caso é necessário calcular por meio do segundo método.
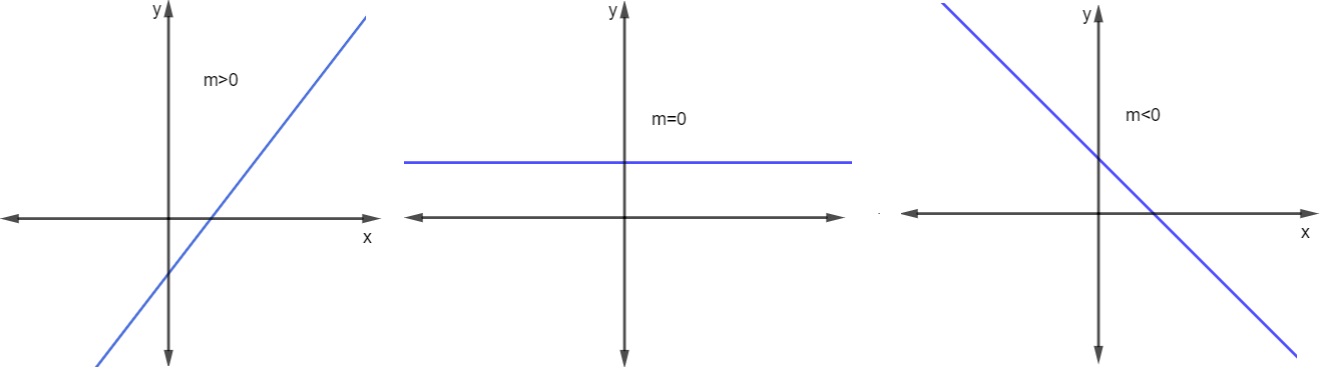
O coeficiente angular nos possibilita analisar se a reta é crescente, decrescente ou constante. Assim,
m > 0, a reta será crescente;
m = 0 a reta será constante;
m < 0 a reta será decrescente.
Leia também: Distância entre dois pontos
Coeficiente linear
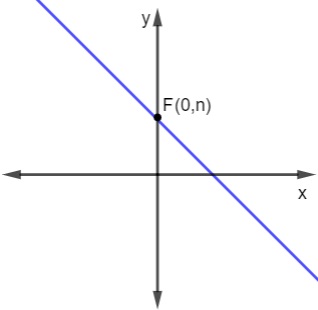
O coeficiente linear n é o valor da ordenada quando x = 0. Isso significa que n é o valor de y para o ponto em que a reta intercepta o eixo y. Graficamente, para encontrar o valor de n, basta encontrar o valor de y no ponto (0,n).
Como calcular a equação reduzida da reta
Para encontrarmos a equação reduzida da reta, é necessário encontrar o valor de m e de n. Encontrando o valor do coeficiente angular e conhecendo um de seus pontos, é possível encontrar o coeficiente linear com facilidade.
Exemplo:
- Encontre a equação da reta que passa pelos pontos A (2,2) e B (3,4).
→ 1º passo: encontrar o coeficiente angular m.
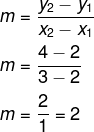
→ 2º passo: encontrar o valor de n.
Para encontrar o valor de n, precisamos de um ponto (podemos escolher entre o ponto A e B) e do valor do coeficiente angular.
Sabemos que a equação reduzida é y = mx + n. Calculamos m = 2 e, utilizando o ponto B(3,4), vamos substituir o valor de x,y e m.
y = mx + n
4 = 2·3 + n
4 = 6 + n
4 – 6 = n
n = – 2
→ 3º passo: escrever a equação substituindo o valor de n e m, que agora são conhecidos.
y = 2x – 2
Essa será a equação reduzida da nossa reta.
Leia também: Ponto de interseção entre duas retas
Exercícios resolvidos
Questão 1 - (Enem 2017) Em um mês, uma loja de eletrônicos começa a obter lucro já na primeira semana. O gráfico representa o lucro (L) dessa loja desde o início do mês até o dia 20. Mas esse comportamento se estende até o último dia, o dia 30.
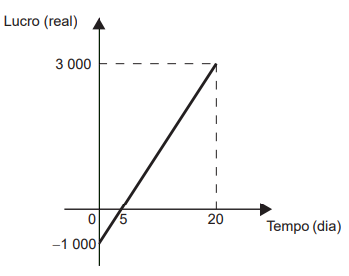
A representação algébrica do lucro (L) em função do tempo (t) é:
a) L(t) = 20t + 3 000
b) L(t) = 20t + 4 000
c) L(t) = 200t
d) L(t) = 200t – 1 000
e) L(t) = 200t + 3 000
Resolução:
Analisando o gráfico, é possível perceber que já temos o coeficiente linear n, pois ele é o ponto em que a reta toca o eixo y. Nesse caso, n = - 1 000.
Agora analisando os pontos A (0, -1000) e B (20, 3 000), calcularemos o valor de m.
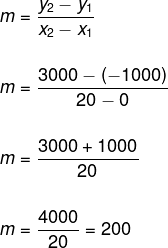
Logo, L(t) = 200t – 1000.
Letra D
Questão 2 - A diferença entre o valor do coeficiente linear e o coeficiente angular da reta crescente que passa pelo ponto (2,2) e faz um ângulo de 45º com o eixo x é de:
a) 2
b) 1
c) 0
d) -1
e) -2
Resolução:
→ 1º passo: calcular o coeficiente angular.
Como conhecemos o ângulo, sabemos que:
m = tgα
m = tg45º
m = 1
→ 2º passo: encontrar o valor do coeficiente linear.
Seja m = 1 e A (2,2), realizando a substituição na equação reduzida, temos que:
y = mx + n
2 = 2 ·1 + n
2= 2 + n
2 – 2 = n
n = 0
→ 3º passo: calcular a diferença na ordem que foi pedida, ou seja, n – m.
0 – 1 = –1
Letra D
Por Raul Rodrigues de Oliveira
Professor de Matemática






