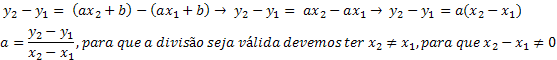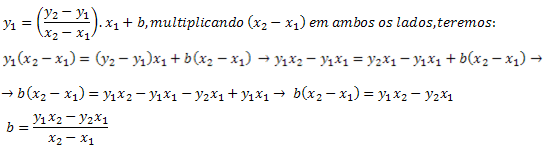Vamos determinar a função que passa por dois pontos. Para isso, precisamos encontrar as coordenadas destes dois pontos, sendo que a coordenada y’ é determinada pelo valor da função na coordenada x’ (x1, f(x1)), (x2, f(x2)).
Pela definição de função afim, temos que ela é determinada pela seguinte expressão f(x)=ax+b, ou seja, para determinar tal função, basta encontrarmos os coeficientes a, b. Veremos que para descobrir estes coeficientes precisamos apenas de dois pontos e o valor da função nesses pontos.
Antes de mostrarmos a expressão do caso geral, vejamos como proceder em um exemplo.
Não pare agora... Tem mais depois da publicidade ;)
Com f(1)=4 e f(2)=6, temos, então, dois pontos e os valores da função nestes pontos.
Para f(1) temos: f(1) = 4 = a.1+b
Para f(2) temos: f(2) = 6 = a.2+b
Destacaremos essas duas relações de igualdade:
6=2a+b (-), se subtrairmos uma igualdade da outra, teremos o seguinte resultado:
4=a+b
2=a, ou seja, a é igual a 2. Descobrimos o valor de um dos coeficientes. Para encontrarmos o outro, basta substituirmos o resultado em uma das igualdades. Usaremos a segunda:
4=a+b
como a=2 teremos , 4=2+b assim teremos, b=2
Como f(x)=ax+b e a=2 e b=2, temos que esta função, para f(1)=4 e f(2)=6, será a seguinte:
f(x)=2x+b.
Mas este é o processo realizado para um caso específico. Como seria a expressão para determinarmos os valores dos coeficientes de qualquer função? Veremos agora.
Seja y1=f(x1) e y2=f(x2), sendo estes pontos, pontos distintos. Teremos que a expressão destes pontos será dada da seguinte forma:
y1=f(x1)=ax1+b
y2=f(x2)=ax2+b, faça a subtração da expressão debaixo pela de cima. Com isso, teremos:
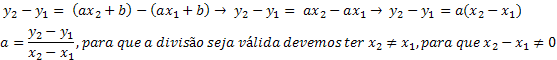
Tendo a expressão para o coeficiente a, substituiremos a expressão para esse coeficiente em y1.
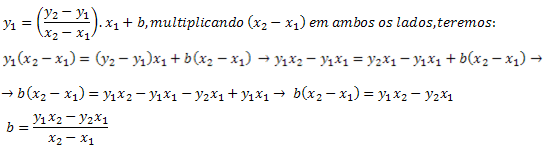
Desta forma, veja que as expressões para os coeficientes a, b, são determinadas apenas pelos valores dos pontos, valores estes que conhecemos.
Com isso, vimos que é possível determinar uma função afim, conhecendo apenas os valores de dois pontos.
Por Gabriel Alessandro de Oliveira
Graduado em Matemática
Equipe Brasil Escola
Matriz e determinante - Matemática - Brasil Escola