Desde os primeiros contatos com a geometria, aprendemos a calcular a área de um triângulo através de sua fórmula geral (base x altura, e o resultado dividido por dois). Entretanto, conforme avançamos nos estudos dos conceitos matemáticos, aprendemos várias expressões e relações que podem ser estabelecidas neste gigantesco mundo da matemática. Hoje veremos que é possível calcular a área de um triângulo sem conhecer o valor da sua altura, necessitando apenas das medidas de dois lados e o ângulo destes lados.
Para isso, vamos desenhar um triângulo qualquer (?ABC), cujos lados valem (b e c) e o ângulo entre eles tem valor igual a Â.
Não pare agora... Tem mais depois da publicidade ;)
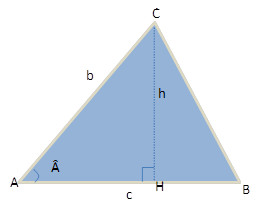
Sabemos que a área deste triângulo deve ser calculada pela expressão:
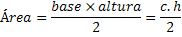
Podemos notar que o triângulo formado pelos vértices ACH é um triângulo retângulo, com isso podemos usar os conceitos trigonométricos de um triângulo retângulo.
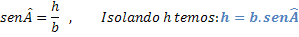
Como temos esta expressão para a altura em relação à hipotenusa e ao seno do ângulo, podemos substituí-la na nossa primeira fórmula para a área.
Com isso, teremos,
.png)
Como você pode ver, a área então fica dada em função da medida dos lados que conhecemos e do seno do ângulo entre estes lados. Lembre-se que os coeficientes (b e c) representam a medida que você conhece.
Esta expressão é denominada de Teorema das Áreas: “A área do triângulo é igual ao semiproduto das medidas de dois lados pelo seno do ângulo formado por estes lados”.
Com isso, você já sabe: se está difícil encontrar o valor da altura para calcular a área, e você possui as informações suficientes para utilizar esta fórmula que aprendemos hoje, não perca tempo, pois ela facilitará o cálculo.
Por Gabriel Alessandro de Oliveira
Graduado em Matemática
Equipe Brasil Escola
Geometria Plana - Matemática - Brasil Escola



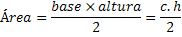
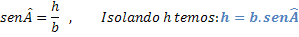
.png)
