O arranjo simples é um tipo de agrupamento estudado na análise combinatória. Conhecemos como arranjo todos os agrupamentos formados com n elementos tomados de k em k, sabendo que o valor de n > k.
Para diferençar o arranjo dos outros agrupamentos (a combinação e a permutação), é importante compreender que, na combinação, a ordem dos elementos no conjunto não é importante e que, no arranjo ela é. Além disso, na permutação, todos os elementos do conjunto estão envolvidos, já no arranjo, escolhemos parte do conjunto, no caso, expresso por k elementos do conjunto.
Para calcular qualquer um desses agrupamentos e, em especial, o arranjo, é necessário a utilização de fórmulas específicas para cada um deles. Existem várias aplicações de arranjo, uma delas é na elaboração de senhas bancárias. Você já se perguntou quantas senhas são possíveis de se criar com certos números e letras? É por meio do arranjo que conseguimos responder a essa pergunta.
Leia também: O que é o princípio fundamental da contagem?

Tópicos deste artigo
- 1 - Qual a fórmula do arranjo simples?
- 2 - Como calcular o arranjo simples?
- 3 - Arranjo simples e combinação simples
- 4 - Exercícios resolvidos
Qual a fórmula do arranjo simples?
Existem problemas de arranjo em que não é necessário utilizar a fórmula, por serem problemas simples. Por exemplo, dado o conjunto {a, b, c}, de quantas formas distintas podemos escolher 2 elementos desse conjunto de forma que a ordem seja importante?
Para resolver esse problema, basta reescrevermos os agrupamentos possíveis. Trata-se de um arranjo porque estamos pegando sequências de 2 elementos de um conjunto que possui 3 elementos. Os arranjos possíveis são:
A{(a, b); (b, a); (a, c); (c, a); (a, d); (d, a); (b, c); (c, b); (b, d); (d, b); (c, d); (d, c)}
Nesse caso podemos dizer que existem 12 arranjos possíveis, com 3 elementos tomados de 2 em 2. Muitas vezes o interesse está na quantidade de arranjos possíveis e não na lista, como fizemos anteriormente.
Para resolver problemas de arranjo, ou seja, encontrar quantos arranjos existem de n elementos tomados de k em k, utilizamos a seguinte fórmula:
![]()
Como calcular o arranjo simples?
Para contar a quantidade de arranjos em uma determinada situação, basta identificar quantos elementos têm no conjunto e quantos elementos serão escolhidos desse conjunto, ou seja, qual o valor de n e qual é o valor de k na situação, posteriormente basta substituir na fórmula os valores encontrados e calcular os fatoriais.
Exemplo 1:
Quantos arranjos existem de 9 elementos tomados de 3 em 3?
n = 9 e k = 3
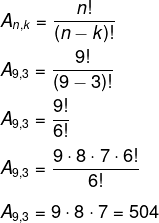
Exemplo 2:
As senhas de um determinado banco são formadas por quatro dígitos, sendo que os algarismos utilizados não poderiam aparecer duas vezes na mesma senha. Sendo assim, qual e a quantidade de senhas possíveis para esse sistema?
Estamos lidando com um problema de arranjo, pois, em uma senha, a ordem é importante, e há 10 opções de algarismos (todos os números de 0 até 9), dos quais escolheremos 4.
n = 10
k = 4
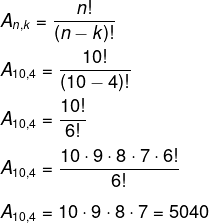
Leia também: Princípio aditivo da contagem — união de um ou mais conjuntos
Arranjo simples e combinação simples
Para quem está estudando análise combinatória, um dos pontos mais importantes é a diferenciação entre problemas que podem ser resolvidos com arranjo simples e problemas que podem ser resolvidos com combinação simples. Embora sejam conceitos próximos e usados para calcular o total de agrupamentos possíveis em uma parte dos elementos do conjunto, para diferenciar problemas envolvendo-os, basta analisar se, no problema proposto, a ordem é importante ou não.
Quando a ordem é importante, o problema é resolvido por meio de um arranjo. O arranjo (A, B) é um agrupamento diferente de (B, A). Desse modo, problemas que envolvem filas, pódio, senhas ou qualquer outra situação em que, ao mudar-se a ordem dos elementos, forma-se agrupamentos diferentes, são resolvidos utilizando a fórmula do arranjo.
Quando a ordem não é importante, o problema é resolvido por meio de uma combinação. A combinação {A, B} é o mesmo agrupamento que {B, A}, ou seja, a ordem dos elementos é irrelevante. Problemas envolvendo sorteio, amostras de um conjunto, entre outros, em que a ordem não é relevante, são resolvidos por meio da fórmula da combinação. Para saber mais detalhes sobre essa outra forma de agrupamento, leia: Combinação simples.
Exercícios resolvidos
Questão 1 - O xadrez surgiu no século VI, na Índia, alcançando outros países, como a China e a Pérsia, e se tornando um dos jogos de tabuleiro mais populares da atualidade, sendo prática de milhões de pessoas e existindo torneios e competições internacionais. O jogo é praticado sobre um tabuleiro quadrado e dividido em 64 casas, alternadamente brancas e pretas. De um lado, ficam as 16 peças brancas, e, de outro, um mesmo número de peças pretas. Cada jogador tem direito a um lance por vez. O objetivo da partida é dar o xeque-mate no adversário. Em uma competição internacional, os 15 melhores enxadristas são igualmente capazes de chegar à final e ser o vencedor. Sabendo disso, de quantas maneiras distintas o pódio dessa competição pode acontecer?
A) 32.760
B) 455
C) 3510
D) 2730
E) 210
Resolução
Alternativa D
Temos que n = 15 e k = 3.
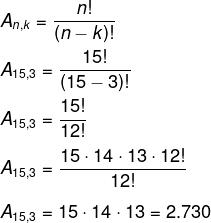
Questão 2 – (Enem) Doze times se inscreveram em um torneio de futebol amador. O jogo de abertura do torneio foi escolhido da seguinte forma: primeiro foram sorteados 4 times para compor o Grupo A. Em seguida, entre os times do Grupo A, foram sorteados 2 times para realizar o jogo de abertura do torneio, sendo que o primeiro deles jogaria em seu próprio campo, e o segundo seria o time visitante. A quantidade total de escolhas possíveis para o Grupo A e a quantidade total de escolhas dos times do jogo de abertura podem ser calculadas por meio de:
A) uma combinação e um arranjo, respectivamente.
B) um arranjo e uma combinação, respectivamente.
C) um arranjo e uma permutação, respectivamente.
D) duas combinações.
E) dois arranjos.
Resolução
Alternativa A. Para saber qual o tipo de agrupamento a que o problema está se referindo, basta analisar se a ordem é importante ou não.
No primeiro agrupamento, serão sorteados 4 times entre os 12. Note que, nesse sorteio, a ordem não importa. Independentemente da ordem, os 4 times sorteados vão compor o Grupo A, logo, o primeiro agrupamento é uma combinação.
Já na segunda escolha, dos 4 times serão sorteados 2, porém o primeiro jogará em casa, logo, nesse caso, a ordem gera resultados diferentes, tratando-se, então, de um arranjo.
Por Raul Rodrigues Oliveira
Professor de Matemática

